Lab 07 Examples (Summation, Recursion)¶

Click <shift> <enter> in each code cell to run the code. Be sure to start with the #include directives to load the required libraries.

In [1]:

// For Lab 07, we are limited to using only <iostream> and <string>

#include <iostream>
#include <string>

An Overview of Today's Lab¶

Today's lab will involve implementing four functions.

The first is a summation that will be calculated using a formula.
The second will perform the same summation using iteration (a loop).
The third will perform the same summation using recursion.
The fourth will be a recursive function to calculate the nth Fibonacci number. We will look at this function in detail in these notes, so the point is for you to understand the recursion rather than to reinvent how it works on your own.

Summation¶

Given a positive integer n, we want the sum of the first n natural numbers: $$S(n)=\sum_{k=1}^{n} k$$

The formula for this summation is:¶

$$S(n) = \frac{n(n + 1)}{2}$$

Examples¶

$$S(5) = \frac{5(5 + 1)}{2} = 15$$

$$S(4) = \frac{4(4 + 1)}{2} = 10$$

$$S(1) = \frac{1(1 + 1)}{2} = 1$$

Iterative approach¶

Accumulate the sum by looping from 1 to n.
Unlike the formula, which is a constant time operation O(1), this approach takes linear time O(n). Regardless of the number being calculated, the formula will take the same amount of time. The loop, however, will take longer as n increases.

Examples¶

$$S(5) = 1 + 2 + 3 + 4 + 5 = 15$$ $$S(4) = 1 + 2 + 3 + 4 = 10$$ $$S(1) = 1$$

Recursion¶

A recursive function is a function that calls itself. Like iteration (using loops), recursion allows for repeating a set of instructions multiple times. And while recursion can be used for mere repetition, it is often better suited for problems that can be broken down into smaller instances of the same problem.

Just as a loop can be infinite if the exit condition is never met, a recursive function can also be infinite if there is no base case to stop the recursion.

int a = 0;
while (a >= 0) {
    std::cout << "This loop will run forever!" << std::endl;
}

void infiniteRecursion() {
    std::cout << "This function will continuously call itself until it runs out of memory." << std::endl;
    infiniteRecursion();
}

While the loop will continue until the program is manually interrupted, the recursive function will eventually produce a stack overflow error when the program runs out of memory to store the function calls. Whenever a function is called, a new frame is added to the call stack to manage the function's parameters and local variables. Since there's no base case in which the function will end without again calling itself, the stack keeps growing until its memory capacity is reached.

A stack is a data structure that follows a Last In, First Out (LIFO) order. When an item is added to the stack, it is pushed onto the top. When an item is removed, it is popped from the top. This can be visualized as a stack of cafeteria trays. When a new tray is added to the stack of trays, it is set on top of the existing trays. When a tray is removed, it is removed from the top.

A recursive function will therefore typically have two main components:

A recursive case that breaks the problem down into smaller instances of itself.
A base case that stops the recursion, allowing the call stack to unwind.

Here is a recursive function that counts down from a given number to zero:

In [2]:

void countdown(int n) {
    if (n == 0) // base case
        return;
    std::cout << n << std::endl;
    countdown(n - 1); // recursive call
}

// start countdown from 10
countdown(10);

While using recursion for simple tasks like counting down from a given number is possible, it's not the most suitable approach. Here a loop would be simpler. But there are problems that are more inherently recursive, and for such problems, the recursive solution can be the simpler and more elegant one.

Finding the nth Fibonacci number is a classic example of a problem that can be solved recursively, and in which the recursive solution is often more concise than the iterative one.

The Fibonacci Sequence¶

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. The sequence typically begins as follows:

$$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...$$

$f(0) = 0$ and $f(1) = 1$ are the defined base cases.

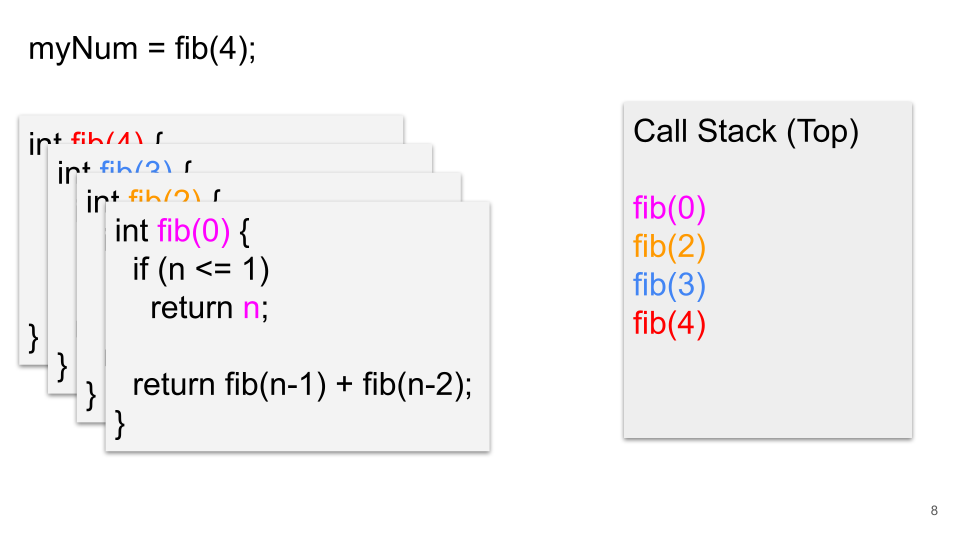
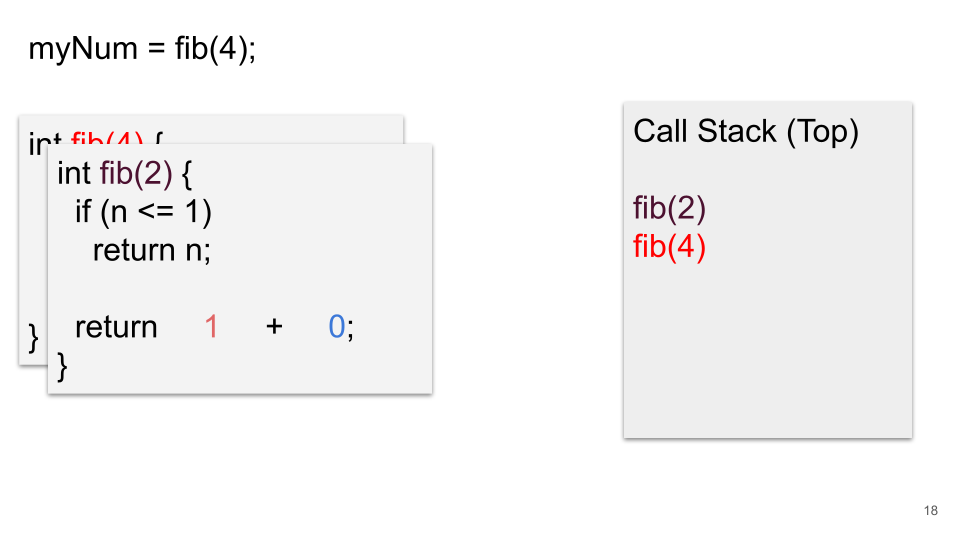
We will now step through the recursive Fibonacci function as it calculates the 4th Fibonacci number. We will take note of each recursive call, as it is pushed onto and popped off the call stack.