Lab 02 Examples¶

Click <shift> <enter> in each code cell to run the code. Be sure to start with the #include directives to load the required libraries.

In [1]:
// For Lab 02, we are limited to these includes.
// Other libraries that can do the set or binary operations for us are not allowed.
// For example, DO NOT include <bitset> or <set>.

#include <iostream>
#include <string>
#include <vector>
#include <cmath>

The Exclusive OR (XOR) Operator¶

Last week we discussed the AND and OR operators.

True AND True = True
True AND False = False
False AND True = False
False AND False = False

True OR True = True
True OR False = True
False OR True = True
False OR False = False

In English, when we say OR, we usually mean either or, meaning one or the other but not both. The logical OR, however, means one or the other or both. If we intend to mean one or the other exclusively, we use the Exclusive OR (XOR) operator. In C++, the XOR operator is represented by the caret ^.

True XOR True = False
True XOR False = True
False XOR True = True
False XOR False = False
In [2]:
std::cout << "True XOR True: " << (true ^ true) << std::endl;     // Outputs 0 (false)
std::cout << "True XOR False: " << (true ^ false) << std::endl;   // Outputs 1 (true)
std::cout << "False XOR True: " << (false ^ true) << std::endl;   // Outputs 1 (true)
std::cout << "False XOR False: " << (false ^ false) << std::endl; // Outputs 0 (false)

True XOR True: 0
True XOR False: 1
False XOR True: 1
False XOR False: 0
Out[2]:
@0x7a67e89fcca0
In [3]:
std::cout << "1 ^ 2     = " << (1 ^ 2) << std::endl;     // Outputs 3
std::cout << "1 ^ 4     = " << (1 ^ 4) << std::endl;     // Outputs 5
std::cout << "2 ^ 4     = " << (2 ^ 4) << std::endl;     // Outputs 6
std::cout << "1 ^ 2 ^ 4 = " << (1 ^ 2 ^ 4) << std::endl; // Outputs 7

1 ^ 2     = 3
1 ^ 4     = 5
2 ^ 4     = 6
1 ^ 2 ^ 4 = 7
Out[3]:
@0x7a67e89fcca0
Operation Result (Binary) Result (Base 10)
001 ⊕ 010 011 3
001 ⊕ 100 101 5
010 ⊕ 100 110 6
001 ⊕ 010 ⊕ 100 111 7

Hamming Code (7,4)¶

  • Hamming code is a method to detect and correct single-bit errors in a block of data. The (7,4) Hamming code takes 4 data bits and adds 3 parity bits to create a 7-bit codeword.
  • The 7 refers to the total number of bits in the codeword.
    • The 4 refers to the number of data bits.
    • The 3 refers to the number of parity bits used for error detection and correction.
    • In an 8-bit byte, one bit remains unused. However, Hamming code (7,4) can be extended to (8,4) to make use of all 8 bits.
      • Hamming code (8,4) can detect if a second error is present, but it cannot locate or correct the second error.
  • If more than two bits are altered, hamming code may misinterpret the data.

At first glance, it might seem inefficient to use 3 parity bits for just 4 data bits. However, as the amount of data increases, the efficiency of the Hamming code improves. For example, Hamming code (7, 4) uses 3 parity bits for 4 data bits. Hamming code (15, 11) uses 4 parity bits for 11 data bits. Hamming code (31, 26) uses 5 parity bits for 26 data bits. Hamming code (63, 57) uses 6 parity bits for 57 data bits.

With 3 parity bits, we can accommodate 4 data bits. $2^3 = 8$, which is sufficient to cover the 4 data bits and the 3 parity bits.
With 4 parity bits, we can accommodate 11 data bits. $2^4 = 16$, which is sufficient to cover the 11 data bits and the 4 parity bits.
With 5 parity bits, we can accommodate 26 data bits. $2^5 = 32$, which is sufficient to cover the 26 data bits and the 5 parity bits.
With 6 parity bits, we can accommodate 57 data bits. $2^6 = 64$, which is sufficient to cover the 57 data bits and the 6 parity bits.

The parity bits are placed at indexes that are powers of 2 (1, 2, 4, 8, etc).

At every power of 2, binary counting adds a new bit position. The parity bits are placed at the first index number requiring a new bit position.

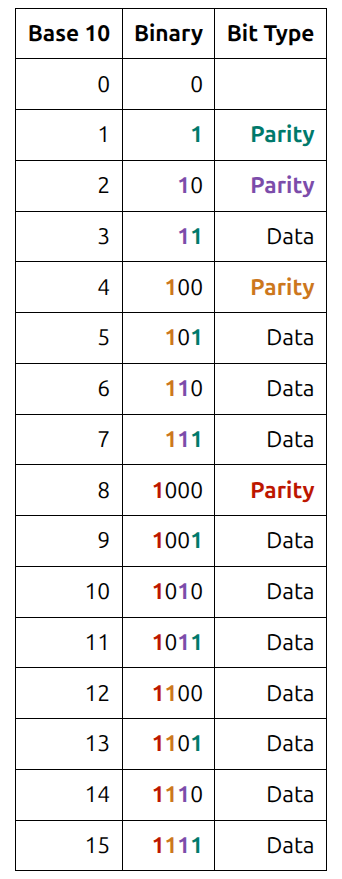
Hamming Code Parity Bits

The parity bits are responsible for checking data bits with a 1 in their respective bit position.

In Hamming code (7,4), the parity bit at index 1 checks the bits at indexes 1, 3, 5, and 7.
In Hamming code (7,4), the parity bit at index 2 checks the bits at indexes 2, 3, 6, and 7.
In Hamming code (7,4), the parity bit at index 4 checks the bits at indexes 4, 5, 6, and 7.

Let's consider an example.

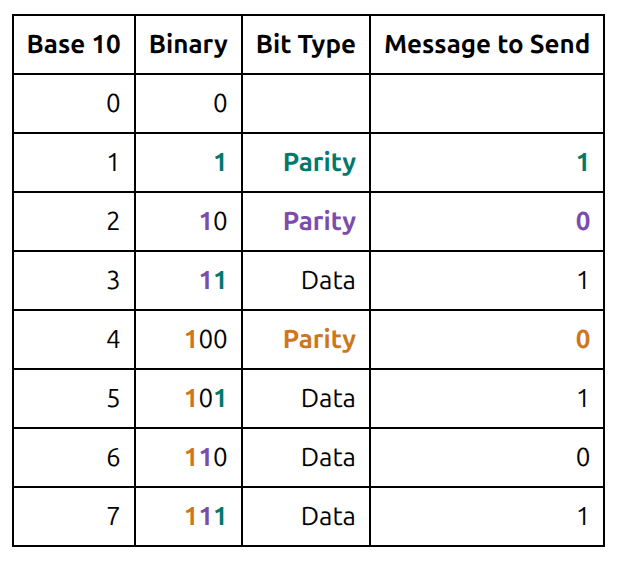
Encoding the message 1101 using Hamming code (7,4)¶

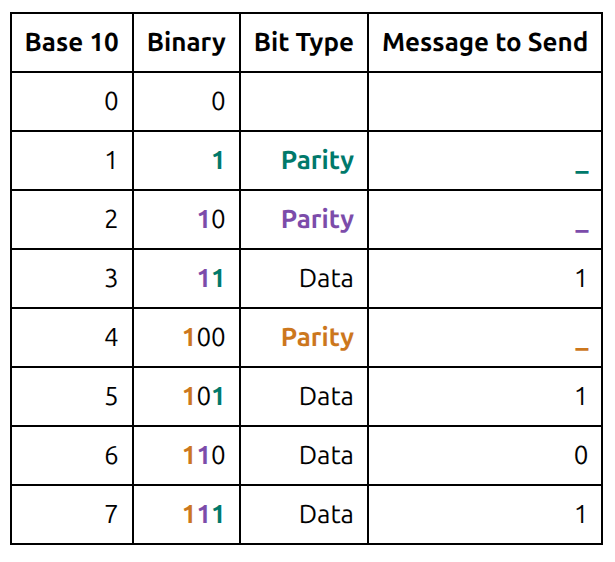
Hamming Code Example of Bits to Send (Parity Bits Blank)

Fill in the parity bits, so the respective parity groups have even parity (an even number of 1s).

Hamming Code Example of Bits to Send (Parity Bits Filled In)

Detecting and Correcting a Single-Bit Error¶

Let's assume we encounter a single bit error, and the message sent as 1101 is received as 1111. The bit at index 6 has erroneously flipped from 0 to 1.

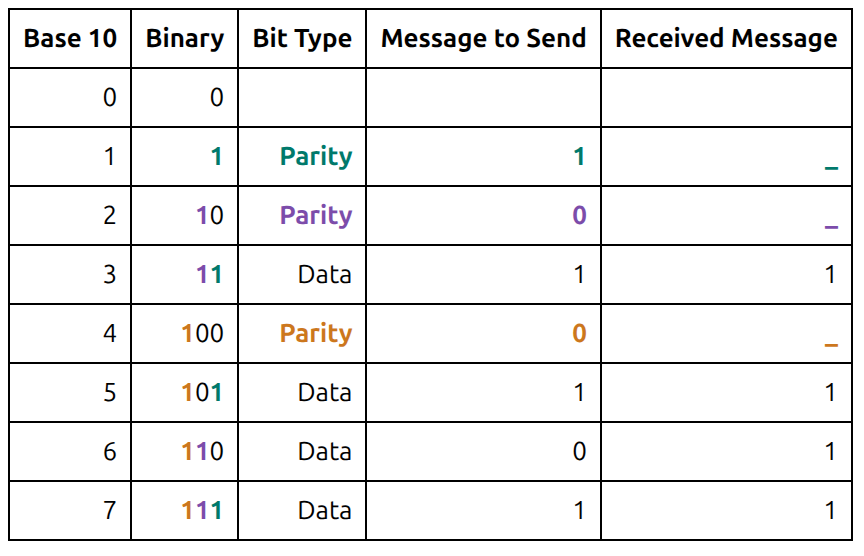
Hamming Code Example of Bits Received (Recalculated Parity Bits Blank)

Recalculate the parity bits on the received message.

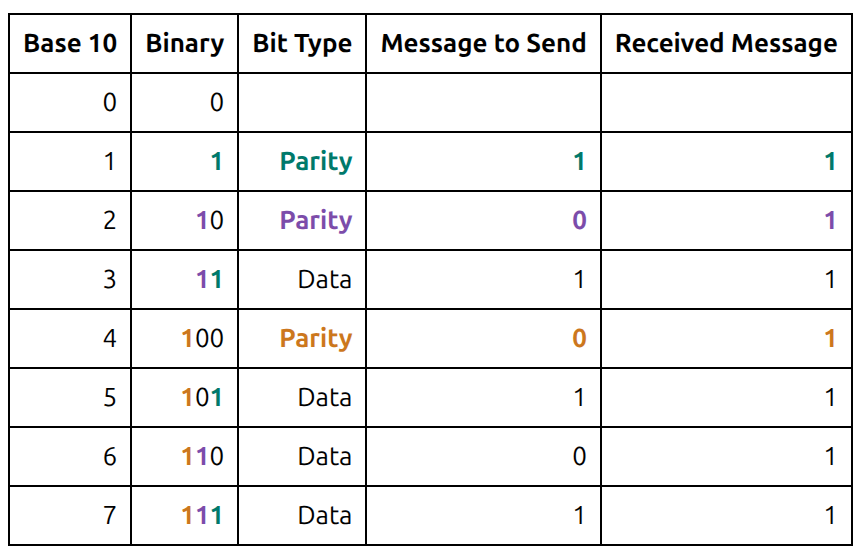
Hamming Code Example of Bits Received (Recalculated Parity Bits Filled In)

Parity bit 1 is the same on the sent message as it is on the received message, so there is no error in the bits it checks (1, 3, 5, 7).
Parity bit 2 is different on the sent message than it is on the received message, so there is an error in one of the bits it checks (2, 3, 6, 7).
Parity bit 4 is different on the sent message than it is on the received message, so there is an error in one of the bits it checks (4, 5, 6, 7).

  • Looking at a Venn diagram, we can see that everything from parity group 1 is OK. {1, 3, 5, 7}.
  • Parity group 2 reports that {2, 3, 6, 7} could be the error, but it won't be {3} or {7} because group 1 reported those indexes OK. {2} and {6} remain suspicious.
  • Parity group 4 reports that {4, 5, 6, 7} could be the error, but it won't be {5} or {7} because group 1 reported those indexes OK. {4} and {6} remain suspicious.
  • However, the error can't be index {4} because group 2 reported an error and group 2 doesn't cover index {4}.
  • And the error can't be index {2} because group 4 reported an error and group 4 doesn't cover index {2}.
  • The error must be index {6}.
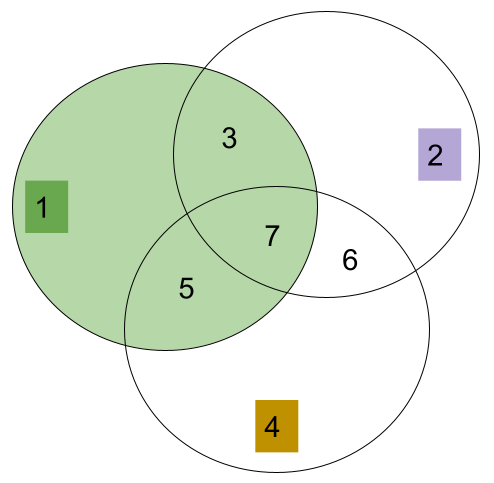
Hamming Code Venn Diagram

We successfully identified the error, but looking at a diagram to visually deduce the index is not the most programmatic approach. To implement this as a computer program, could we leverage a more programmatic operation?

Using Set Operations¶

Treat the parity groups as sets and codeword indexes as set members.

  • Both notations below show the same operation.
  • The bar over ONE indicates the complement (also known as the inverse) and can be achieved with the ! symbol in C++.
  • The superscript C indicates the complement using set notation.

$$(\text{TWO} \cap \text{FOUR}) \cap \overline{\text{ONE}}$$

$$(\{2, 3, 6, 7\} \cap \{4, 5, 6, 7\}) \cap \{1, 3, 5, 7\}^C = \{6\}$$

We detected the error at codeword index 6, and can now correct it by flipping it back to 0!

A Strategy to Identify Parity Group Membership¶

  • The parity bit can act as a bit mask, and along with the bitwise & operation, identify which indexes belong to which parity groups.
  • Remember, Zero is considered false. Non-Zero is considered true.
Parity Group 1 Bit Mask Decimal Equivalent Membership
001 & 001 = 0011 & 1 = 1Group 1 Parity Bit
001 & 010 = 0001 & 2 = 0NOT In Group
001 & 011 = 0011 & 3 = 1In Group
001 & 100 = 0001 & 4 = 0NOT In Group
001 & 101 = 0011 & 5 = 1In Group
001 & 110 = 0001 & 6 = 0NOT In Group
001 & 111 = 0011 & 7 = 1In Group
Parity Group 2 Bit Mask Decimal Equivalent Membership
010 & 001 = 002 & 1 = 0NOT In Group
010 & 010 = 102 & 2 = 2Group 2 Parity Bit
010 & 011 = 102 & 3 = 2In Group
010 & 100 = 002 & 4 = 0NOT In Group
010 & 101 = 002 & 5 = 0NOT In Group
010 & 110 = 102 & 6 = 2In Group
010 & 111 = 102 & 7 = 2In Group
Parity Group 4 Bit Mask Decimal Equivalent Membership
100 & 001 = 0004 & 1 = 0NOT In Group
100 & 010 = 0004 & 2 = 0NOT In Group
100 & 011 = 0004 & 3 = 0NOT In Group
100 & 100 = 1004 & 4 = 4Group 4 Parity Bit
100 & 101 = 1004 & 5 = 4In Group
100 & 110 = 1004 & 6 = 4In Group
100 & 111 = 1004 & 7 = 4In Group
In [4]:
std::cout << "Parity Group 1 Membership" << std::endl;
std::cout << "1 & 1 = " << (1 & 1) << std::endl; // Group 1 Parity Bit
std::cout << "1 & 2 = " << (1 & 2) << std::endl; // Not in Group
std::cout << "1 & 3 = " << (1 & 3) << std::endl; // In Group
std::cout << "1 & 4 = " << (1 & 4) << std::endl; // Not in Group
std::cout << "1 & 5 = " << (1 & 5) << std::endl; // In Group
std::cout << "1 & 6 = " << (1 & 6) << std::endl; // Not in Group
std::cout << "1 & 7 = " << (1 & 7) << std::endl; // In Group

std::cout << "\nParity Group 2 Membership" << std::endl;
std::cout << "2 & 1 = " << (2 & 1) << std::endl; // Not in Group
std::cout << "2 & 2 = " << (2 & 2) << std::endl; // Group 2 Parity Bit
std::cout << "2 & 3 = " << (2 & 3) << std::endl; // In Group
std::cout << "2 & 4 = " << (2 & 4) << std::endl; // Not in Group
std::cout << "2 & 5 = " << (2 & 5) << std::endl; // Not in Group
std::cout << "2 & 6 = " << (2 & 6) << std::endl; // In Group
std::cout << "2 & 7 = " << (2 & 7) << std::endl; // In Group

std::cout << "\nParity Group 4 Membership" << std::endl;
std::cout << "4 & 1 = " << (4 & 1) << std::endl; // Not in Group
std::cout << "4 & 2 = " << (4 & 2) << std::endl; // Not in Group
std::cout << "4 & 3 = " << (4 & 3) << std::endl; // Not in Group
std::cout << "4 & 4 = " << (4 & 4) << std::endl; // Group 4 Parity Bit
std::cout << "4 & 5 = " << (4 & 5) << std::endl; // In Group
std::cout << "4 & 6 = " << (4 & 6) << std::endl; // In Group
std::cout << "4 & 7 = " << (4 & 7) << std::endl; // In Group

Parity Group 1 Membership
1 & 1 = 1
1 & 2 = 0
1 & 3 = 1
1 & 4 = 0
1 & 5 = 1
1 & 6 = 0
1 & 7 = 1

Parity Group 2 Membership
2 & 1 = 0
2 & 2 = 2
2 & 3 = 2
2 & 4 = 0
2 & 5 = 0
2 & 6 = 2
2 & 7 = 2

Parity Group 4 Membership
4 & 1 = 0
4 & 2 = 0
4 & 3 = 0
4 & 4 = 4
4 & 5 = 4
4 & 6 = 4
4 & 7 = 4
Out[4]:
@0x7a67e89fcca0

For Your Consideration...¶

  • What does it mean if there are no non-matching parity bits?
  • Your codeword is stored in a data structure such as an array or a vector. For example, {1, 0, 1, 0, 1, 0, 1}. How will you unload these 0 and 1 bits from an array or vector into a single base-10 integer value to print the corrected message?

Examine the following line of pseudocode:

  x = 0
  x = x | ( (codeword[power(2, i)] ^ codeword_recalculated[power(2, i)]) * power(2, i) )
  • What is this line calculating? What does x represent?
  • What is the purpose of the OR (|) operation in this context?
  • What is the purpose of the XOR (^) operation in this context?
  • Why is the result of the XOR operation multiplied by 2 to the power of i (presumably an incrementing loop index)?

See if you can answer these questions on your own, and check in with me if you get stuck. We'll analyze a solution together next week.